Chapitre 11 Test indépendance

Les tests d’indépendances permettent de définir s’il existe un lien entre deux variables. Il existe différent test d’indépence, en voici quelques exemples :

Test indépendance entre deux variables quantitatives / Test de corrélation Pearson
Test d’indépendance entre deux variables qualitatives / Test du Chi²
Test d’indépendance entre une variable qualitative et une quantitative / Test de Fisher avec l’analyse de la variance (ANOVA)

11.1 Test de corrélation

L’intérêt des tests de corrélation est d’apporter plus de pertinence et fiabilité aux coefficients de corrélation. Il existe différents test de corrélation, nous utilisons celui de Pearson.

On travaille avec le jeu de données fromage 🧀 disponible en cliquant ici.

df <- read.csv(file = "./dataset/fromage.txt", sep = "\t", row.names = 1)

	calories	sodium	calcium	lipides	retinol	folates	proteines	cholesterol	magnesium
CarredelEst	314	353.5	72.6	26.3	51.6	30.3	21.0	70	20
Babybel	314	238.0	209.8	25.1	63.7	6.4	22.6	70	27
Beaufort	401	112.0	259.4	33.3	54.9	1.2	26.6	120	41
Bleu	342	336.0	211.1	28.9	37.1	27.5	20.2	90	27
Camembert	264	314.0	215.9	19.5	103.0	36.4	23.4	60	20
Cantal	367	256.0	264.0	28.8	48.8	5.7	23.0	90	30

plot(df)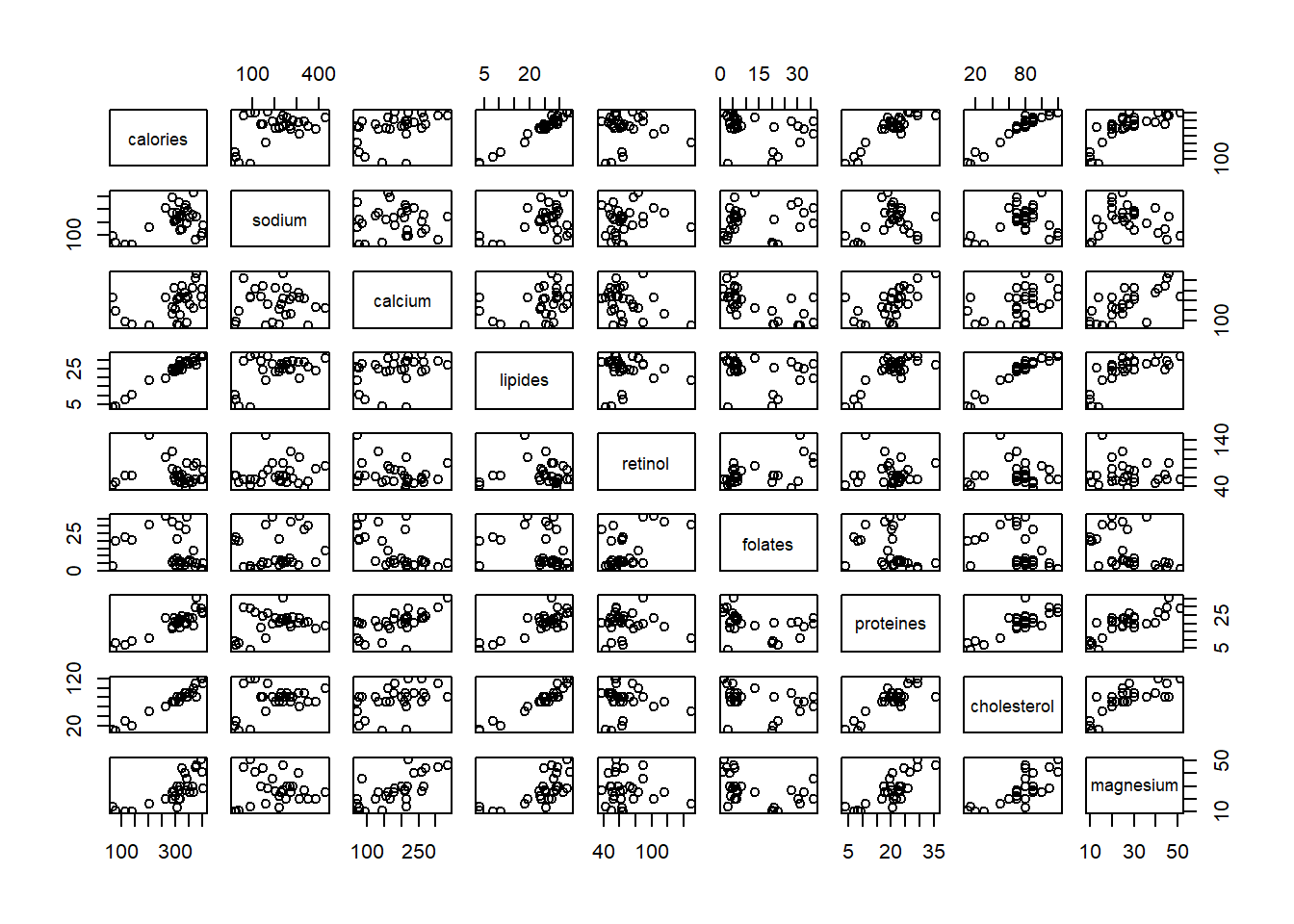

library(corrplot)
corrplot(cor(df, method = "pearson"))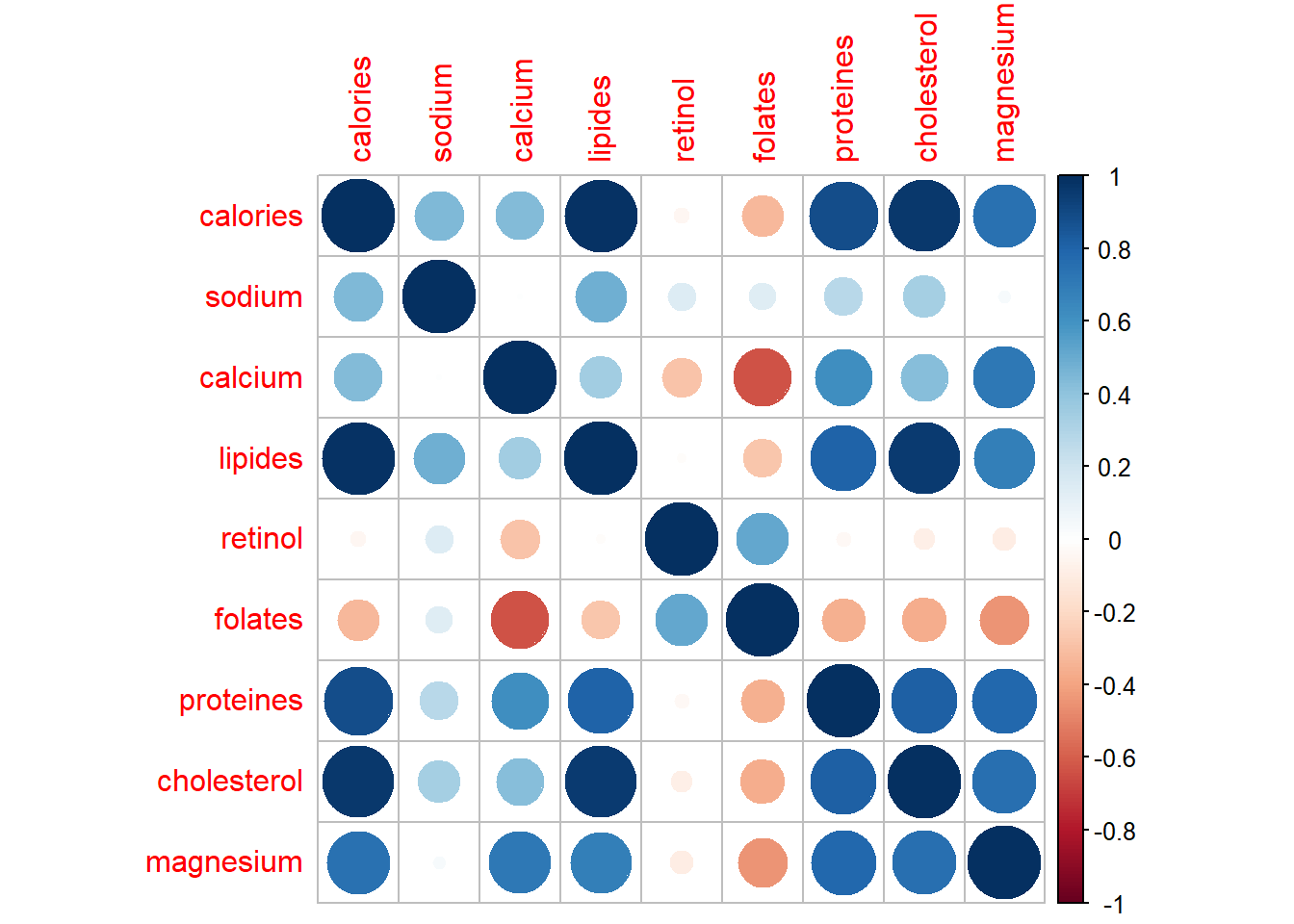

On pose les hypothèses de départ :

H0 : Variables indépendantes si p-value > 5%
H1 : Variables non indépendantes si p-value < 5%

11.1.1 Lipide vs Magnesium

La première sortie correspond au coefficient de corrélation, la seconde à la p-value (ou probabilité critique)

cor(x = df$lipides, y = df$magnesium)

## [1] 0.6898601

cor.test(x = df$lipides, y = df$magnesium)

## 
##  Pearson's product-moment correlation
## 
## data:  df$lipides and df$magnesium
## t = 4.9515, df = 27, p-value = 3.469e-05
## alternative hypothesis: true correlation is not equal to 0
## 95 percent confidence interval:
##  0.4327766 0.8431785
## sample estimates:
##       cor 
## 0.6898601

H1 : Variables non indépendantes

11.1.2 Sodium vs Retinol

cor.test(x = df$sodium, y = df$retinol)

## 
##  Pearson's product-moment correlation
## 
## data:  df$sodium and df$retinol
## t = 0.75788, df = 27, p-value = 0.4551
## alternative hypothesis: true correlation is not equal to 0
## 95 percent confidence interval:
##  -0.2345870  0.4851693
## sample estimates:
##       cor 
## 0.1443276

H0 : Variables indépendantes si p-value > 5%

Si on veut rejeter H0 et prendre H1, j’ai 45,5% de chance de me tromper

Les tests statistiques sont trés sensibles à la taille de l’échantillon. Un coefficient de corrélation de 0.14 n’aura pas la même significativité sur un échantillon de 29 fromages qu’un échantillon de 319 fromages avec le même coefficient de corrélation.

On construit un dataframe en dupliquant le nombre de lignes

sodium <- rep(df$sodium,times = 10)
retinol <- rep(df$retinol,times = 10)
nom <- rep(rownames(df),times = 10)

df_10 <- data.frame(nom,sodium,retinol)

Chaque fromage apparaît plusieurs fois, on a augmenté la taille de l’échantillon

table(df_10$nom)

## 
##            Babybel           Beaufort               Bleu          Camembert 
##                 10                 10                 10                 10 
##             Cantal        CarredelEst          Chabichou           Chaource 
##                 10                 10                 10                 10 
##            Cheddar              Comte        Coulomniers               Edam 
##                 10                 10                 10                 10 
##           Emmental Fr.chevrepatemolle        Fr.fondu.45     Fr.frais20nat. 
##                 10                 10                 10                 10 
##     Fr.frais40nat.          Maroilles            Morbier           Parmesan 
##                 10                 10                 10                 10 
##      Petitsuisse40        PontlEveque           Pyrenees          Reblochon 
##                 10                 10                 10                 10 
##         Rocquefort        SaintPaulin               Tome           Vacherin 
##                 10                 10                 10                 10 
## Yaourtlaitent.nat. 
##                 10

On effectue un autre test de corrélation avec les mêmes variables sur l’échantillon plus grand.

cor.test(x = df_10$sodium, y = df_10$retinol)

## 
##  Pearson's product-moment correlation
## 
## data:  df_10$sodium and df_10$retinol
## t = 2.4752, df = 288, p-value = 0.01389
## alternative hypothesis: true correlation is not equal to 0
## 95 percent confidence interval:
##  0.0296407 0.2552637
## sample estimates:
##       cor 
## 0.1443276

H1 : Variables non indépendantes

On obtient logiquement le même coefficient de corrélation, mais en revanche, cette fois si la p-value est proche de 0.

11.1.3 Matrice des p-values

On effectue un test de corrélation sur chaque variable 2 à 2 en isolant uniquement la p-value

get_pvalue <- function(x,y){
  p <- cor.test(df[,x],df[,y])$p.value
  return(p)
}

colonne <- colnames(df)
ligne <- colnames(df)
df_pvalues <- outer(X = colonne, Y = ligne, FUN = Vectorize(get_pvalue))
colnames(df_pvalues) <- colnames(df)
rownames(df_pvalues) <- colnames(df)

On affiche la matrice des corrélations avec un gradiant de couleur

corrplot(df_pvalues, method="number", type="upper",
         col=colorRampPalette(c("white","red","green"))(3))

11.1.4 Cas de relation non linéaire

Les différents de corrélation sont beaucoup plus adaptés aux relation linéaire. C’est pourquoi il est important de toujours visualiser les distributions (plus d’infos ici).

Cas d’une relation non-linéaire et non-monotone

x <- -10:10
y <- x^2 + rnorm(n = length(x))

plot(x,y)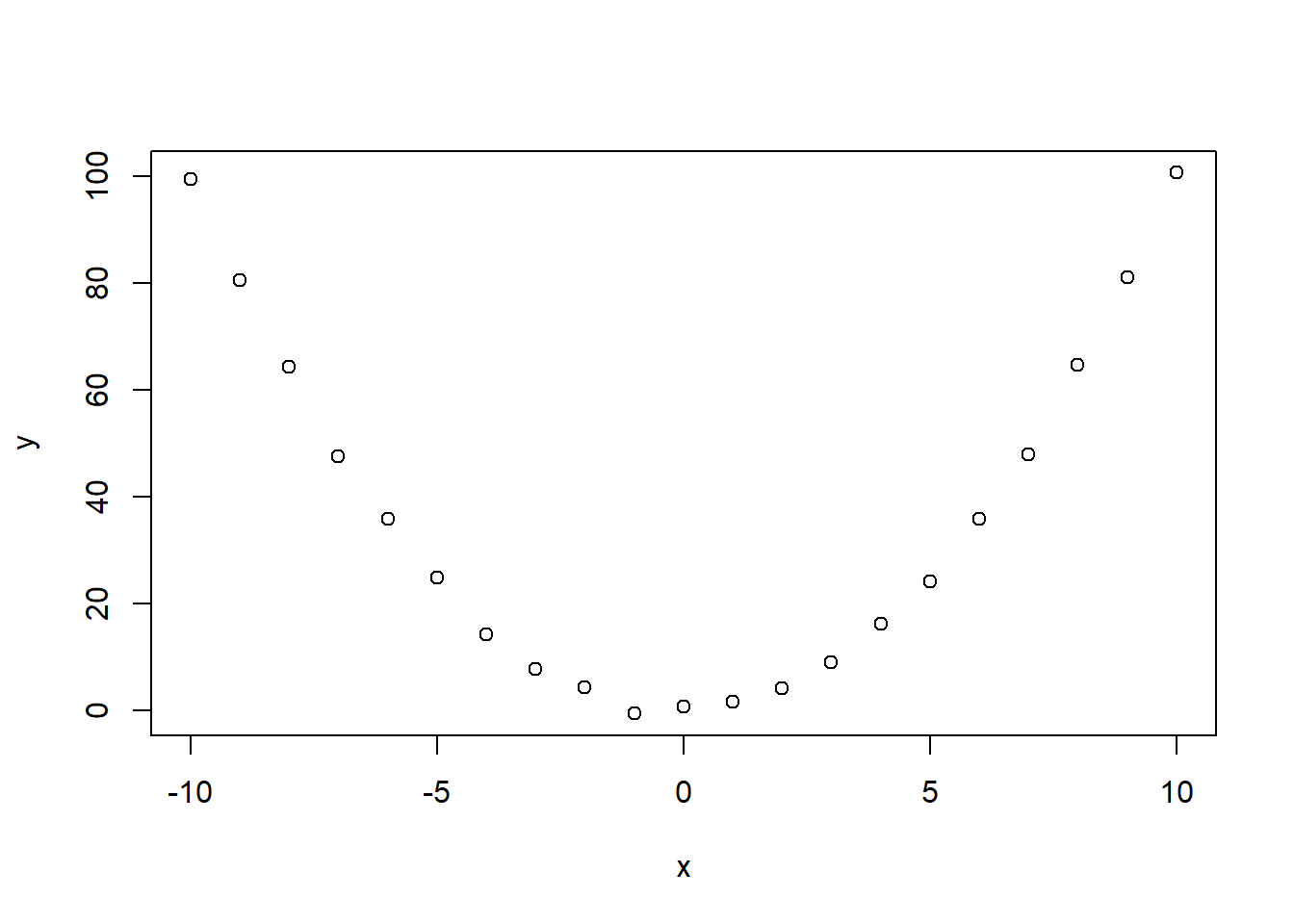

cor.test(x, y, method = "pearson")

## 
##  Pearson's product-moment correlation
## 
## data:  x and y
## t = 0.036055, df = 19, p-value = 0.9716
## alternative hypothesis: true correlation is not equal to 0
## 95 percent confidence interval:
##  -0.4249327  0.4383928
## sample estimates:
##         cor 
## 0.008271336

cor.test(x, y, method = "spearman")

## 
##  Spearman's rank correlation rho
## 
## data:  x and y
## S = 1456, p-value = 0.8148
## alternative hypothesis: true rho is not equal to 0
## sample estimates:
##        rho 
## 0.05454545

cor.test(x, y, method = "kendall")

## 
##  Kendall's rank correlation tau
## 
## data:  x and y
## T = 109, p-value = 0.8347
## alternative hypothesis: true tau is not equal to 0
## sample estimates:
##        tau 
## 0.03809524

11.2 Test du CHI²

L’intérêt du test du Chi² est de mesurer l’indépendance entre deux variables qualitatives à partir de tableau de contigence.

11.2.1 Titanic

On travaille sur le jeu de données Titanic 🧊⛴ disponible en cliquant ici.

df <- read.csv(file = "./dataset/Titanic.csv", row.names = 1)

Name	PClass	Age	Sex	Survived	SexCode
Allen, Miss Elisabeth Walton	1st	29.00	female	1	1
Allison, Miss Helen Loraine	1st	2.00	female	0	1
Allison, Mr Hudson Joshua Creighton	1st	30.00	male	0	0
Allison, Mrs Hudson JC (Bessie Waldo Daniels)	1st	25.00	female	0	1
Allison, Master Hudson Trevor	1st	0.92	male	1	0
Anderson, Mr Harry	1st	47.00	male	1	0

df_count <- table(df$Survived, df$PClass)

On pose :

H0 : Variables indépendantes si p-value > 5%
H1 : Variables non indépendantes si p-value < 5%

resultat <-chisq.test(df$Survived,df$PClass)
resultat

## 
##  Pearson's Chi-squared test
## 
## data:  df$Survived and df$PClass
## X-squared = 172.3, df = 2, p-value < 2.2e-16

H1 : Variables non indépendantes

La fonction attributes permet d’afficher les différentes sorties calculées.

attributes(resultat)

## $names
## [1] "statistic" "parameter" "p.value"   "method"    "data.name" "observed" 
## [7] "expected"  "residuals" "stdres"   
## 
## $class
## [1] "htest"

Par exemple le tableau des effectifs théoriques.

resultat$expected

##            df$PClass
## df$Survived     1st       2nd      3rd
##           0 211.642 184.03656 467.3214
##           1 110.358  95.96344 243.6786

11.2.2 Exemple du support

data <- matrix(rbind(c(693,886,534,153),c(597,696,448,95)),ncol=4)
data

##      [,1] [,2] [,3] [,4]
## [1,]  693  886  534  153
## [2,]  597  696  448   95

chisq.test(data)

## 
##  Pearson's Chi-squared test
## 
## data:  data
## X-squared = 6.0504, df = 3, p-value = 0.1092

H0 : Variables indépendantes

Si on veut rejeter H0 et prendre H1, j’ai 10,9% de chance de me tromper

Lecture dans la table du Chi2

p <- seq(0.80, 0.90, 0.005)
dof <- seq(1,3)
chisq_table <- outer(p, dof, function(x,y) qchisq(x,y))
chisq_table <- t(chisq_table)
colnames(chisq_table) <- 1 - p
rownames(chisq_table) <- dof
chisq_table <- round(chisq_table,2)

0.2	0.195	0.19	0.185	0.18	0.175	0.17	0.165	0.16	0.155	0.15	0.145	0.14	0.135	0.13	0.125	0.12	0.115	0.11	0.105	0.1
1.64	1.68	1.72	1.76	1.80	1.84	1.88	1.93	1.97	2.02	2.07	2.12	2.18	2.23	2.29	2.35	2.42	2.48	2.55	2.63	2.71
3.22	3.27	3.32	3.37	3.43	3.49	3.54	3.60	3.67	3.73	3.79	3.86	3.93	4.00	4.08	4.16	4.24	4.33	4.41	4.51	4.61
4.64	4.70	4.76	4.83	4.89	4.96	5.02	5.09	5.17	5.24	5.32	5.40	5.48	5.56	5.65	5.74	5.83	5.93	6.03	6.14	6.25

📢 Taille de l’échantillon

Les tests d’indépendance sont trés sensibles à la taille des échantillons. Ici on divise par 100 pour avoir des effectifs faibles mais en conservant les répartitions.

chisq.test(data/100)

## 
##  Pearson's Chi-squared test
## 
## data:  data/100
## X-squared = 0.060504, df = 3, p-value = 0.9961

H0 : Variables indépendantes

Ici on multiplie par 100 pour avoir des effectifs grands mais en conservant les répartitions

chisq.test(data*100)

## 
##  Pearson's Chi-squared test
## 
## data:  data * 100
## X-squared = 605.04, df = 3, p-value < 2.2e-16

H1 : Variables non indépendantes

11.3 ANOVA 1

On effectue une analyse de variance pour mesurer l’indépendance entre une variable qualitative et une quantitative.

Pour illustrer cela, on utilise le jeu de données Hotdogs 🌭 disponible en cliquant ici.

df <- read.csv(file = "./dataset/Hotdogs.csv", 
               sep = ";")

Type	Calories	Sodium
Beef	186	495
Beef	181	477
Beef	176	425
Beef	149	322
Beef	184	482
Beef	190	587

On va tester l’indépendance entre la variable qualitative Type et la variable quantitatives Calories.

boxplot(Calories  ~ Type, data = df, 
        horizontal = TRUE)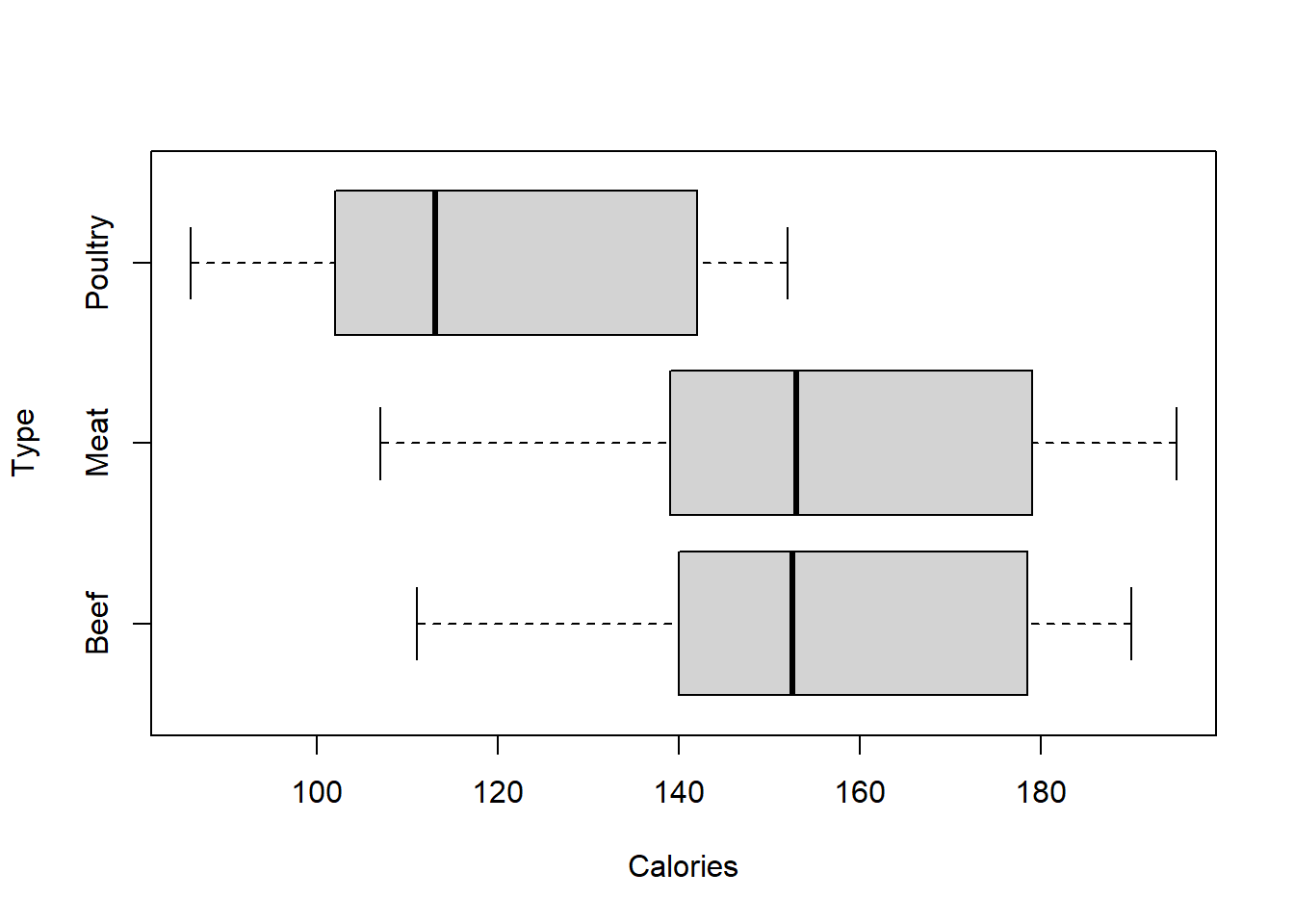

Dans une ANOVA, on cherche à déterminer si les moyennes des groupes sont significativement différentes. On pose donc :

H0 : Les moyennes de chaque groupe sont égales si p-value > 5%
H1 : Les moyennes de chaque groupe ne sont pas toutes égales si p-value < 5%

Dans une ANOVA, on étudie la variance de chacun de ces groupes. Pour cela on utilise la fonction aov().

aov <- aov(formula = Calories ~ Type, data = df)
summary(aov)

##             Df Sum Sq Mean Sq F value   Pr(>F)    
## Type         2  17692    8846   16.07 3.86e-06 ***
## Residuals   51  28067     550                     
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

H1 : Les moyennes de chaque groupe ne sont pas toutes égales

Quand on dispose d’un petit échantillon, la pertinence de ce test repose sur la validation de plusieurs hypothèses :

l’indépendance entre les échantillons de chaque groupe
l’égalité des variances que l’on peut verifier avec un test de Bartlett.
la normalité des résidus avec un test de Shapiro.

11.3.1 L’indépendance

L’indépendance est une des 3 conditions de validité d’une ANOVA. Seul le contexte de l’étude permet de s’assurer de l’indépendance entre les échantillons de chaque groupe (ici beef, poultry, chicken.)

11.3.2 L’égalité des variances

On parle aussi d’homoscédasticité. C’est une des 3 conditions de validité d’une ANOVA. On cherche à démontrer que les variances de chaque groupe sont égales. Dans un boxplot, l’amplitude des boîtes traduit graphiquement l’égalité des variances.

boxplot(Calories  ~ Type, data = df, 
        horizontal = TRUE)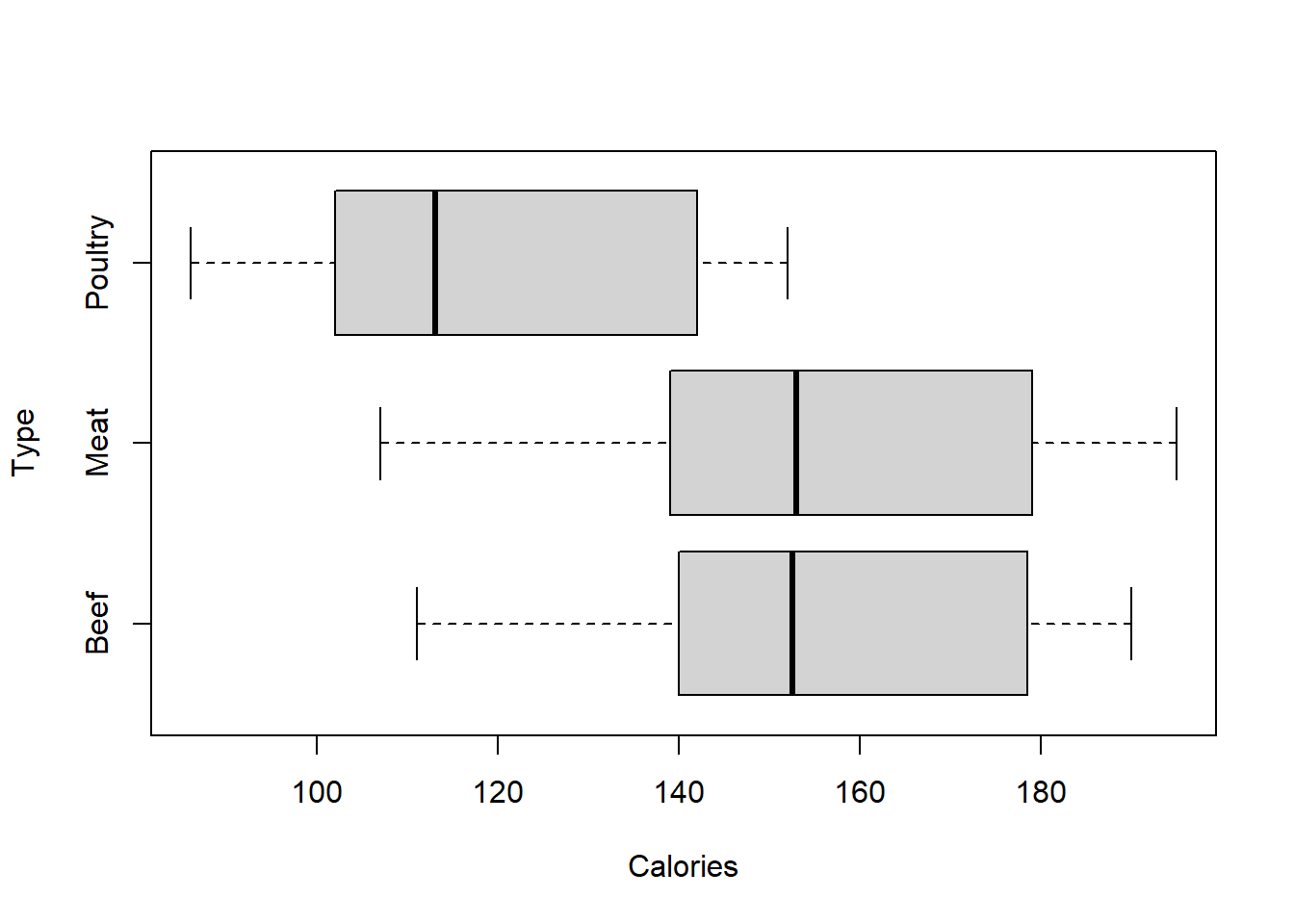

Mais c’est le test de bartlett qui permet de tester si les variances sont significativement différentes ou non avec :

H0 : Les variances de chaque groupe sont égales si p-value > 5%
H1 : Les variances de chaque groupe ne sont pas toutes égales < 5%

bartlett.test(Calories  ~ Type, data = df)

## 
##  Bartlett test of homogeneity of variances
## 
## data:  Calories by Type
## Bartlett's K-squared = 0.26732, df = 2, p-value = 0.8749

H0 : Les variances de chaque groupe sont égales. La deuxième condition pour effectuer une anova est validée.

11.3.3 Normalité des résidus

C’est une des 3 conditions de validité d’une ANOVA. L’objectif est de s’assurer que les résidus suivent une loi normale afin de ne pas affirmer qu’il existe une différence de moyenne entre les groupes qui serait causée par le hasard.

Dans R, on utilise le test de Shapiro-Wilk pour tester la normalité des résidus où :

H0 : Les résidus suivent une loi normale si p-value > 5%
H1 : Les résidus ne suivent pas une loi normale si p-value < 5%

aov <- aov(formula = Calories ~ Type, data = df)
shapiro.test(aov$residuals)

## 
##  Shapiro-Wilk normality test
## 
## data:  aov$residuals
## W = 0.94199, p-value = 0.0113

H1 : Les résidus ne suivent pas une loi normale

11.3.4 Calcul - Cas des variances égales

a <- seq(from = 1, to = 11, length.out = 9   )
b <- seq(from = 31, to = 40, length.out = 9   )
c <- seq(from = 51, to = 62, length.out = 9   )

df <- data.frame(Valeur = c(a,b,c), Groupe = c(rep("A",9),
                        rep("B",9),
                        rep("C",9)))
kable(df)

Valeur	Groupe
1.000	A
2.250	A
3.500	A
4.750	A
6.000	A
7.250	A
8.500	A
9.750	A
11.000	A
31.000	B
32.125	B
33.250	B
34.375	B
35.500	B
36.625	B
37.750	B
38.875	B
40.000	B
51.000	C
52.375	C
53.750	C
55.125	C
56.500	C
57.875	C
59.250	C
60.625	C
62.000	C

boxplot(Valeur  ~ Groupe, data = df, 
        col = 1:3, horizontal = TRUE)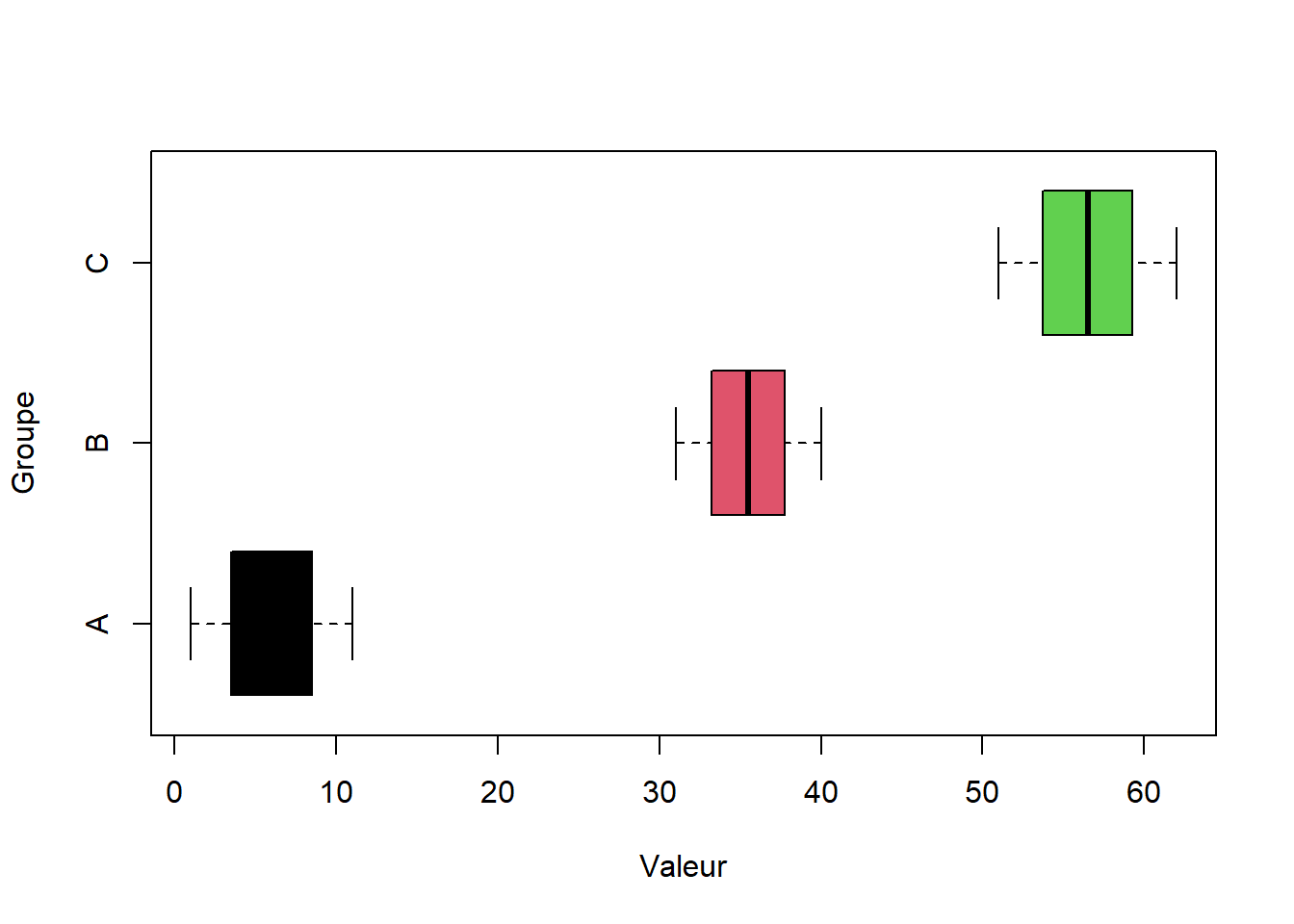

Comment calculer le tableau récaptitulatif de l’analyse de la variance :

##             Df Sum Sq Mean Sq F value Pr(>F)    
## Groupe       2  11585    5792     491 <2e-16 ***
## Residuals   24    283      12                   
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Variance intra classes

SCE_a <- (a - mean(a))^2
SCE_b <- (b - mean(b))^2
SCE_c <- (c - mean(c))^2
intra <- sum(SCE_a + SCE_b + SCE_c)
intra

## [1] 283.125

Variance inter classes

moyenne <- mean(df$Valeur)
moyenne_facteur <- tapply(X = df$Valeur, 
                          INDEX = df$Groupe,
                          FUN = mean)

longueur_facteur <- tapply(X = df$Valeur, 
                           INDEX = df$Groupe,
                           FUN = length)
inter <- sum(longueur_facteur*((moyenne_facteur - moyenne)^2))
inter

## [1] 11584.5

Degré de liberté

n <- nrow(df)
p <- length(levels(df$Groupe))
dof_inter <- p - 1
dof_intra <- n - p
dof_inter

## [1] -1

dof_intra

## [1] 27

Calcul de la statistique de test de Fisher

Stat_Fisher <- (inter/dof_inter) / (intra/dof_intra)
Stat_Fisher

## [1] -1104.747

On lit dans la table de Fisher

pvalue <- 1-pf(q = Stat_Fisher,
   df1 = dof_inter,
   df2 = dof_intra)

## Warning in pf(q = Stat_Fisher, df1 = dof_inter, df2 = dof_intra): Production de
## NaN

pvalue

## [1] NaN

Réciproque de la loi de Fisher pour retrouver la statistique de test.

qf(p = 1-pvalue, df1 = dof_inter, df2 = dof_intra)

## [1] NaN

11.3.5 Calcul - Cas des variances inégales

a <- seq(from = 1, to = 40, length.out = 9   )
b <- seq(from = 10, to = 30, length.out = 9   )
c <- seq(from = 25, to = 30, length.out = 9   )

df <- data.frame(Valeur = c(a,b,c), Groupe = c(rep("A",9),
                        rep("B",9),
                        rep("C",9)))
kable(df)

Valeur	Groupe
1.000	A
5.875	A
10.750	A
15.625	A
20.500	A
25.375	A
30.250	A
35.125	A
40.000	A
10.000	B
12.500	B
15.000	B
17.500	B
20.000	B
22.500	B
25.000	B
27.500	B
30.000	B
25.000	C
25.625	C
26.250	C
26.875	C
27.500	C
28.125	C
28.750	C
29.375	C
30.000	C

boxplot(Valeur  ~ Groupe, data = df, 
        col = 1:3, horizontal = TRUE)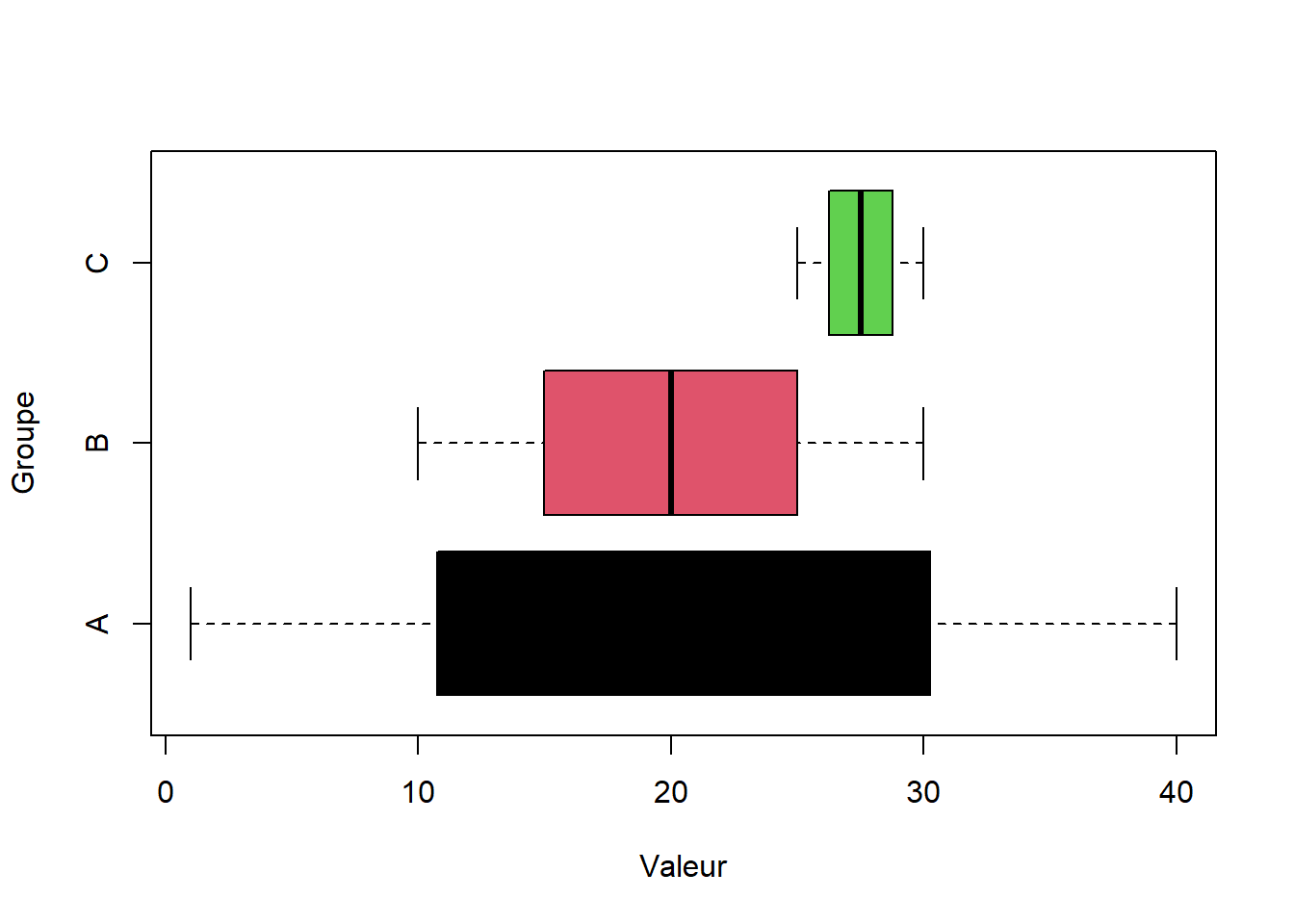

Comment calculer le tableau récaptitulatif de l’analyse de la variance :

##             Df Sum Sq Mean Sq F value Pr(>F)
## Groupe       2  316.5  158.25   2.082  0.147
## Residuals   24 1824.4   76.02

Variance intra classes

SCE_a <- (a - mean(a))^2
SCE_b <- (b - mean(b))^2
SCE_c <- (c - mean(c))^2
intra <- sum(SCE_a + SCE_b + SCE_c)
intra

## [1] 1824.375

Variance inter classes

moyenne <- mean(df$Valeur)
moyenne_facteur <- tapply(X = df$Valeur, 
                          INDEX = df$Groupe,
                          FUN = mean)

longueur_facteur <- tapply(X = df$Valeur, 
                           INDEX = df$Groupe,
                           FUN = length)
inter <- sum(longueur_facteur*((moyenne_facteur - moyenne)^2))
inter

## [1] 316.5

Degré de liberté

n <- nrow(df)
p <- length(levels(df$Groupe))
dof_inter <- p - 1
dof_intra <- n - p
dof_inter

## [1] -1

dof_intra

## [1] 27

Calcul de la statistique de test de Fisher

Stat_Fisher <- (inter/dof_inter) / (intra/dof_intra)
Stat_Fisher

## [1] -4.68407

On lit dans la table de Fisher

pvalue <- 1-pf(q = Stat_Fisher,
   df1 = dof_inter,
   df2 = dof_intra)

## Warning in pf(q = Stat_Fisher, df1 = dof_inter, df2 = dof_intra): Production de
## NaN

pvalue

## [1] NaN

Réciproque de la loi de Fisher pour retrouver la statistique de test.

qf(p = 1-pvalue, df1 = dof_inter, df2 = dof_intra)

## [1] NaN

11.4 ANOVA 2

Même principe que l’Anova à un facteur sauf qu’on ajoute un autre facteur. L’idée est de tester l’indépendance de ces facteurs sur une variable quantitatives continue.

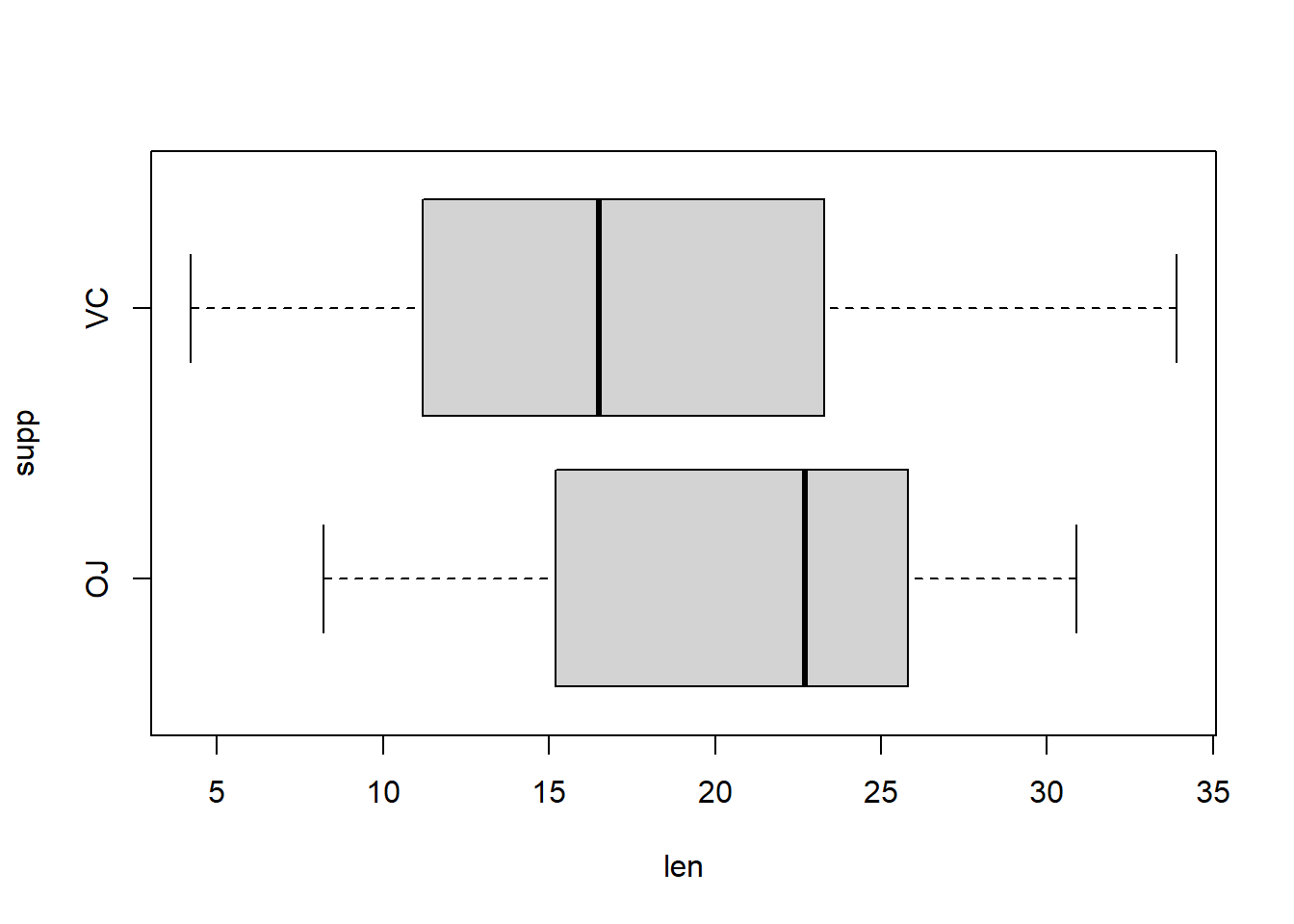
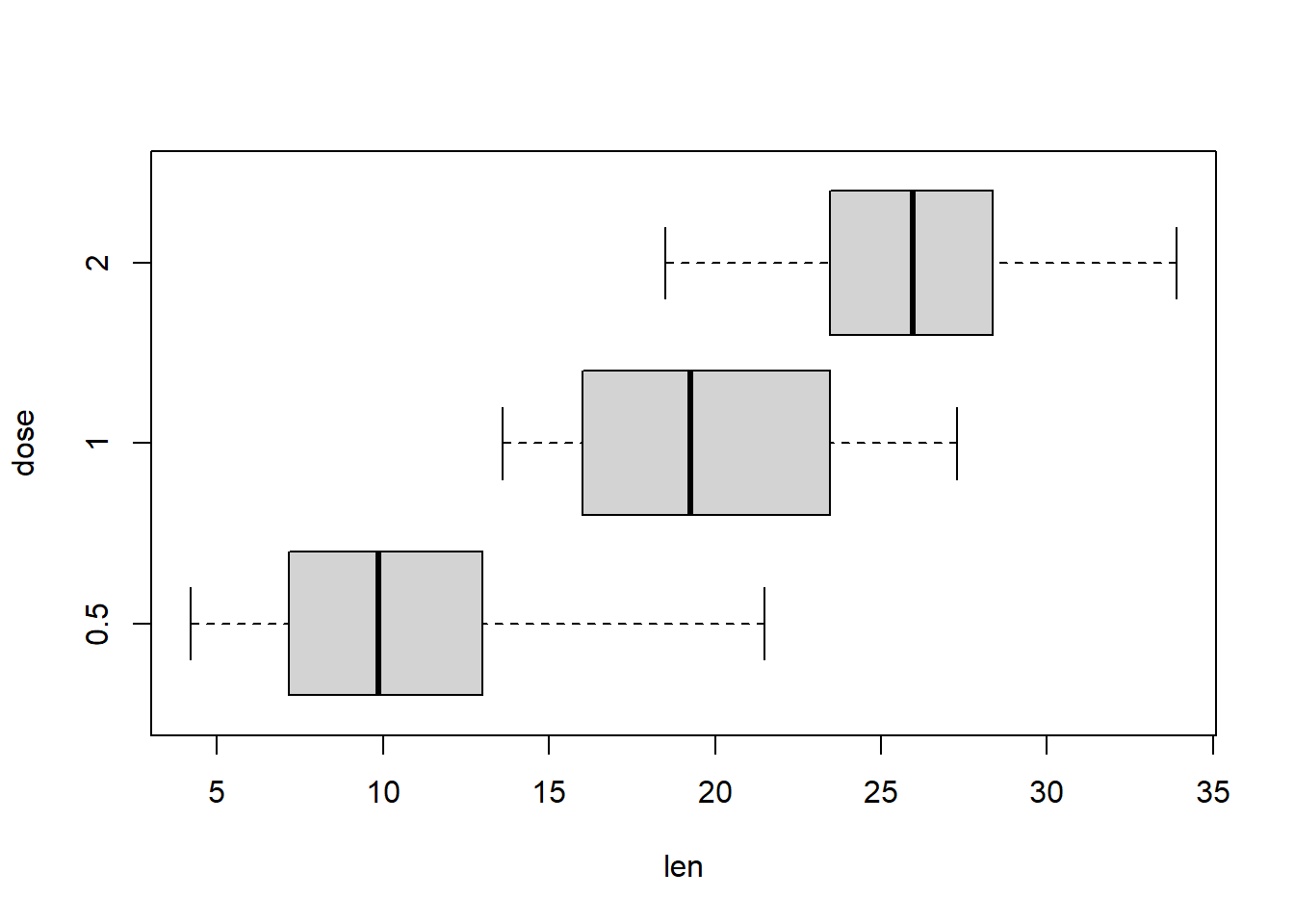
On étudie la longueur des odontoblastes (cellules responsables de la croissance dentaire) chez 60 cobayes. Chaque animal a reçu l’une des trois doses de vitamine C (0,5, 1 et 2 mg / jour) par l’une des deux méthodes d’administration, du jus d’orange ou de l’acide ascorbique (une forme de vitamine C et codée VC) :

len : lLongueur de la dent
supp : supplément (VC ou OJ).
dose : dose en milligrammes / jour

Ce jeu de données ToothGrowth est présent dans le datasets.

df <- ToothGrowth

len	supp	dose
4.2	VC	0.5
11.5	VC	0.5
7.3	VC	0.5
5.8	VC	0.5
6.4	VC	0.5
10.0	VC	0.5
11.2	VC	0.5
11.2	VC	0.5
5.2	VC	0.5
7.0	VC	0.5
16.5	VC	1.0
16.5	VC	1.0
15.2	VC	1.0
17.3	VC	1.0
22.5	VC	1.0
17.3	VC	1.0
13.6	VC	1.0
14.5	VC	1.0
18.8	VC	1.0
15.5	VC	1.0
23.6	VC	2.0
18.5	VC	2.0
33.9	VC	2.0
25.5	VC	2.0
26.4	VC	2.0
32.5	VC	2.0
26.7	VC	2.0
21.5	VC	2.0
23.3	VC	2.0
29.5	VC	2.0
15.2	OJ	0.5
21.5	OJ	0.5
17.6	OJ	0.5
9.7	OJ	0.5
14.5	OJ	0.5
10.0	OJ	0.5
8.2	OJ	0.5
9.4	OJ	0.5
16.5	OJ	0.5
9.7	OJ	0.5
19.7	OJ	1.0
23.3	OJ	1.0
23.6	OJ	1.0
26.4	OJ	1.0
20.0	OJ	1.0
25.2	OJ	1.0
25.8	OJ	1.0
21.2	OJ	1.0
14.5	OJ	1.0
27.3	OJ	1.0
25.5	OJ	2.0
26.4	OJ	2.0
22.4	OJ	2.0
24.5	OJ	2.0
24.8	OJ	2.0
30.9	OJ	2.0
26.4	OJ	2.0
27.3	OJ	2.0
29.4	OJ	2.0
23.0	OJ	2.0

En théorie, dans une ANOVA à plusieurs facteurs, il faut valider chacune des hypothèses une à une pour chaque facteur. La particularité de l’ANOVA à plusieurs facteurs réside dans la mesure de l’intéraction entre les facteurs pouvant mener à des différences de moyennes entres les groupes.

11.4.1 Effet de la variable `supp`

boxplot(len  ~ supp, data = df,
        horizontal = TRUE)

11.4.2 Effet de la variable `dose`

boxplot(len  ~ dose, data = df,
        horizontal = TRUE)

11.4.3 Effet l’intéraction entre les deux facteurs

Pour visualiser graphiquement l’intéraction, on crée une colonne avec les deux modalités

df$interaction <- paste(df$supp,"-",df$dose)

boxplot(len  ~ interaction, data = df,
        horizontal = TRUE)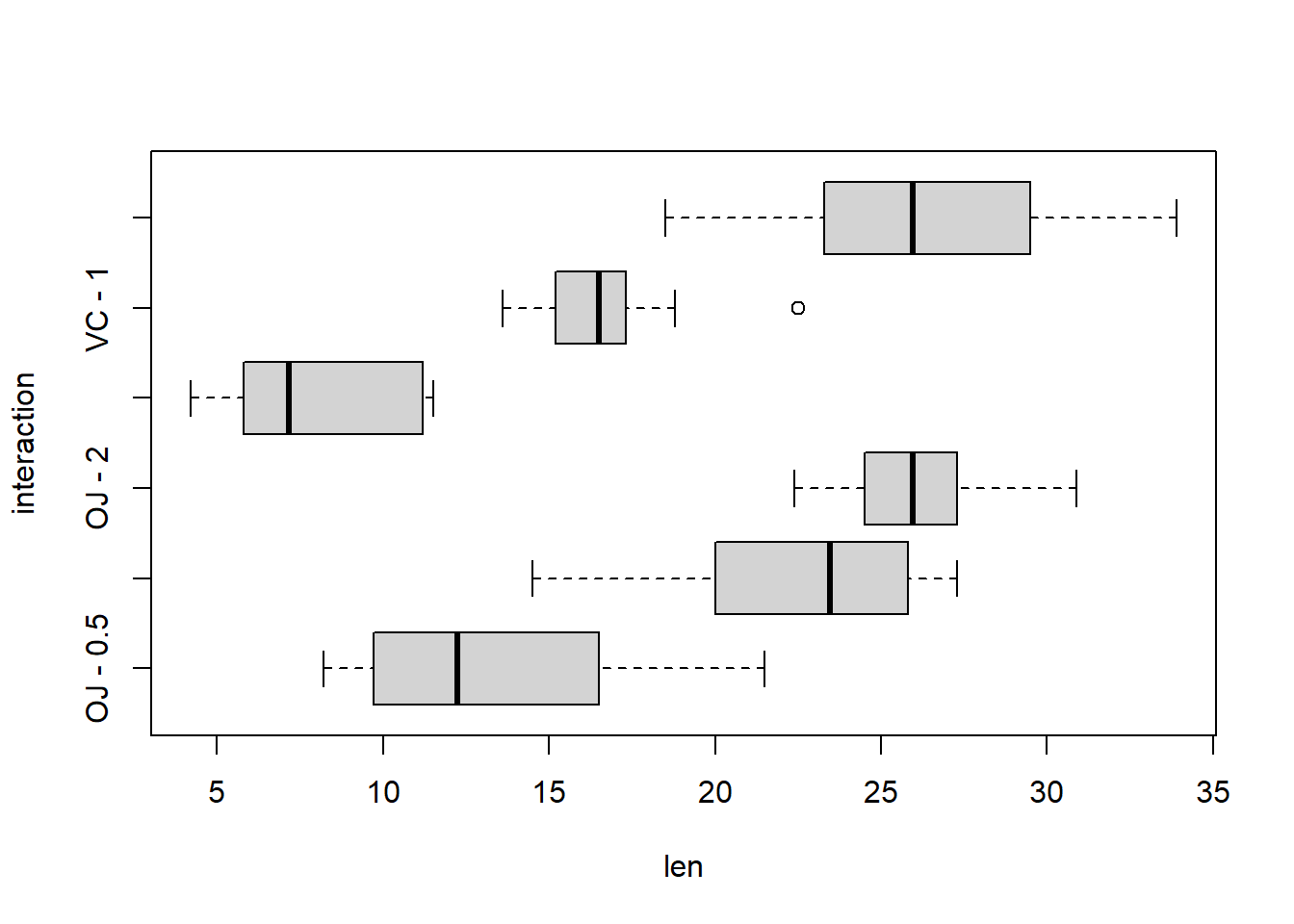

11.4.4 Calcul de l’ANOVA 2

Quelques soit le nombre de facteurs étudiés, nous avons toujours les mêmes hypothèses dans une ANOVA :

H0 : Les moyennes de chaque groupe sont égales si p-value > 5%
H1 : Les moyennes de chaque groupe ne sont pas toutes égales si p-value < 5%

df$dose <- as.factor(df$dose)
aov <- aov(formula = len ~ dose + supp + supp*dose , data = df)
summary(aov)

##             Df Sum Sq Mean Sq F value   Pr(>F)    
## dose         2 2426.4  1213.2  92.000  < 2e-16 ***
## supp         1  205.3   205.3  15.572 0.000231 ***
## dose:supp    2  108.3    54.2   4.107 0.021860 *  
## Residuals   54  712.1    13.2                     
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

H1 : Les moyennes de chaque groupe ne sont pas toutes égales pour chaque facteur.

📢 On voit donc qu’il existe une intéraction entre les deux variables. Pour mesurer quelles associations sont significativement différentes des autres, on peut utilise un test de Tukey qui consiste à faire des tests de comparaison de moyenne sur deux échantillon avec toutes les combinaisons d’association

TukeyHSD(aov)

##   Tukey multiple comparisons of means
##     95% family-wise confidence level
## 
## Fit: aov(formula = len ~ dose + supp + supp * dose, data = df)
## 
## $dose
##         diff       lwr       upr   p adj
## 1-0.5  9.130  6.362488 11.897512 0.0e+00
## 2-0.5 15.495 12.727488 18.262512 0.0e+00
## 2-1    6.365  3.597488  9.132512 2.7e-06
## 
## $supp
##       diff       lwr       upr     p adj
## VC-OJ -3.7 -5.579828 -1.820172 0.0002312
## 
## $`dose:supp`
##                 diff        lwr         upr     p adj
## 1:OJ-0.5:OJ     9.47   4.671876  14.2681238 0.0000046
## 2:OJ-0.5:OJ    12.83   8.031876  17.6281238 0.0000000
## 0.5:VC-0.5:OJ  -5.25 -10.048124  -0.4518762 0.0242521
## 1:VC-0.5:OJ     3.54  -1.258124   8.3381238 0.2640208
## 2:VC-0.5:OJ    12.91   8.111876  17.7081238 0.0000000
## 2:OJ-1:OJ       3.36  -1.438124   8.1581238 0.3187361
## 0.5:VC-1:OJ   -14.72 -19.518124  -9.9218762 0.0000000
## 1:VC-1:OJ      -5.93 -10.728124  -1.1318762 0.0073930
## 2:VC-1:OJ       3.44  -1.358124   8.2381238 0.2936430
## 0.5:VC-2:OJ   -18.08 -22.878124 -13.2818762 0.0000000
## 1:VC-2:OJ      -9.29 -14.088124  -4.4918762 0.0000069
## 2:VC-2:OJ       0.08  -4.718124   4.8781238 1.0000000
## 1:VC-0.5:VC     8.79   3.991876  13.5881238 0.0000210
## 2:VC-0.5:VC    18.16  13.361876  22.9581238 0.0000000
## 2:VC-1:VC       9.37   4.571876  14.1681238 0.0000058

11.4.5 Aller plus loin

Plus d’information sur les tests statistiques ici.

Chapitre 11 Test indépendance

11.1 Test de corrélation

11.1.1 Lipide vs Magnesium

11.1.2 Sodium vs Retinol

11.1.3 Matrice des p-values

11.1.4 Cas de relation non linéaire

11.2 Test du CHI²

11.2.1 Titanic

11.2.2 Exemple du support

11.3 ANOVA 1

11.3.1 L’indépendance

11.3.2 L’égalité des variances

11.3.3 Normalité des résidus

11.3.4 Calcul - Cas des variances égales

11.3.5 Calcul - Cas des variances inégales

11.4 ANOVA 2

11.4.1 Effet de la variable supp

11.4.2 Effet de la variable dose

11.4.3 Effet l’intéraction entre les deux facteurs

11.4.4 Calcul de l’ANOVA 2

11.4.5 Aller plus loin

11.4.1 Effet de la variable `supp`

11.4.2 Effet de la variable `dose`